Ruining the fun: a Wordle auto-solver

Sorry, not sorry.

To cut to the chase: here it is: notfunatparties.com/wordle-solver.

Stop trying to make vetch happen.

Instructions: The Wordle Solver gives you a suggestion. Type this suggestion into Wordle. If you disagree with the suggestion (how dare you), you can change it by clicking on each letter. On the Wordle Solver, click the coloured buttons underneath each letter that matches the feedback you got from Wordle (e.g. Grey, Yellow or Green). The Wordle solver will give you a new suggestion. Repeat until solved.

Disclaimer: You can 100% beat the Solver. It basically never solves the word by the second guess. It pretty much always does it in 4 or 5 though.

A bit of background

If you’ve been on Twitter at all in the past week, you might have seen a bunch of random green, yellow and grey squares, accompanied by some kind of numeric code.

Like this one:

Tom Neill @TomJNeill

Wordle 200 4/6 ⬜⬜🟨🟩⬜ ⬜⬜🟨⬜⬜ ⬜🟨🟨⬜⬜ 🟩🟩🟩🟩🟩 I will admit, I sort of cheated.

(For the uninitiated, go here: powerlanguage.co.uk/wordle, but come back after.)

I did my first one yesterday. I thought pretty well. But as it turns out, my partner beat me, which irked. So I was determined to write some kind of algorithm to do the relationship ruining work for me.

---

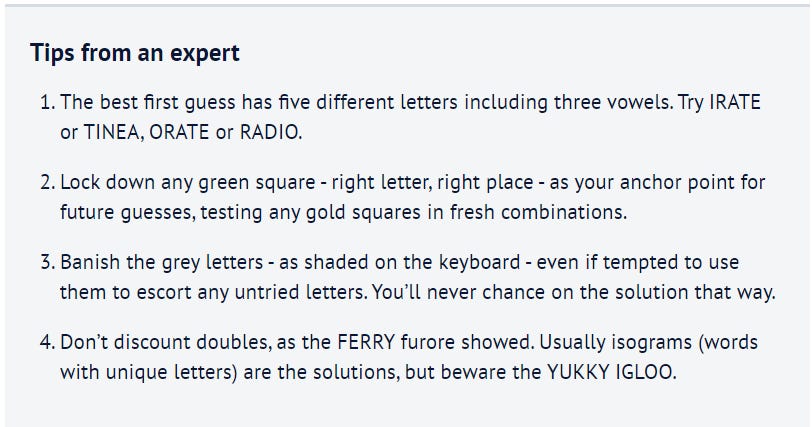
Solver strategy

When I did pretty poorly on my first try, I had a quick look for some “strategy tips”. I found this article in the Sydney Morning Herald, with the following advice:

Unfortunately, this is pretty dumb.

But by looking through Twitter, it’s definitely advice most people follow. If you go through different people’s guessing process, you see a steadily accumulating number of green squares as they gradually fine tune their answers.

I agree with this guy:

Zach Gage @helvetica

it seems like the world disagrees but i’m completely convinced that the best way to play wordle is to guess two words with 10 unique letters for guesses 1 & 2 (unless you’re very sure you can get it on 2). prove me wrong with stats. here’s where i’m at after nearly a month

It’s much better to swing violently from one extreme to another. To try and eliminate as many potential letters and words as quickly as you can. It’s a bit like playing “Guess Who?”.

Or indeed, like some kind of search algorithm…

Writing some kind of search algorithm

I’ve not done this before, so this was fun.

I started with the intuition that at each step, I wanted to eliminate as many words as humanly possible. Clearly, if you guess something like “QUIRK” or “FUZZY”, you’re going to eliminate a lot of words if you get a “Q” or a “Z” correct. But that probably won’t happen. You need to balance the number of words you can eliminate by getting a letter correct with the probability that the word you’re looking for will actually have that letter. Ideally, like in “Guess Who?”, you want your guess’s letter to split the words in half.

For one letter, it’s quite easy to visualise how much better some guesses are than others at splitting the “match vs not-matched” words equally. This is how many words from Wordle’s list start with an “E” (green), have an “E” somewhere else (yellow) or don’t have an “E” (and the same for “Z”):

Guessing “Z” is great iff the word happens to be “Zebra”, “Zesty” or “Zonal”.

It gets a little bit more complicated when you have to create a whole word. You need to start combining the value of multiple letters - and not just the letters themselves, but the order and position of letters within the word. One way to do this is to start assembling some kind of tree diagrams for each word, like this one:

You can fill in the remaining letters

For the first letter, then the second letter, and so on onto the last one, you work out how many words fit all the potential results. For example, how many 5 letter words exist that have neither an “E” or and “R” in them? 846 (according to Wordle). How many start with an “E”, have an “R” in them, but not as the second letter? 20.

If you build these trees out for all five letters, for potentially 243 different paths, you get a measure of the number of words that fit into each bucket. This means you can work out how many words you would expect to have left over if you made this guess.

Assuming that Josh chooses the word from the list randomly, the chance of Wordle giving your guess a particular sequence of 5 colours is equal to the number of words that end up at the right hand side of the tree divided by the total number of words in the list. Again, this example of 2 letters is useful:

Spot the rounding error

Once you’ve done this, you have the probability of every possible response from Wordle to your guess, as well as how many words would fit each possible clue. If you multiple them together and add them up, you get the “expected words remaining” after your guess. Calculate that for every word in the list, take the lowest one, then guess that word.

You can use this method to calculate the best possible first guess for every game. The answer: “RAISE”¹. After that, you need to use the feedback from previous words to change your guess (obviously). Fortunately, you can use exactly the same method. You just need to first filter the list for all the words that could potentially match the previous results.

You could try do all these 562,575 calculations in your head, but fortunately, I have a computer and I can write a bit of hacky JavaScript. This code (which powers the solver), goes through all these steps for each letter, each word and each guess.

If you play with the solver, you can see how the code leads to some pretty interesting guesses. For example, if the word you’re trying to guess is “SEIZE”. After the first guess, you’ve got a pretty good idea of a lot of the letters, and the code says there’s only 15 possible words left. At which point, it recommends guessing “PLANT”, even though that can’t possibly be correct.

But, eliminating all these letters means that by the next word, there’s only 1 possible answer left:

In general I think it’s pretty cool how quickly the words get narrowed down. Even just by using “RAISE” as the first guess, you eliminate almost 98% of potential words on average.

It would be fun to go through all the words and work out what the most difficult potential answer would be. I’ve not found any that take more than 6 guesses, but would be very interested to see if anyone else can.

---

Going through the code

If you’re the kind of person who likes reading code snippets, this might be interesting. However, I’m pretty sure you could make this code a lot better, and certainly a lot more performant.

There’s 2 or 3 “clever” bits that are the most interesting.

Firstly, a function to filter the word list based on all previous criteria:

const matchesFilters = (wordList, filters) => {
  return wordList.filter((word) => {
    let match = true;
    for (let i = 0; i < filters.length; i += 1) {
      const { colour, position, letter } = filters[i];
      if (colour === "black") {
        if (word.includes(letter)) {
          match = false;
          break;
        }
      }
      if (colour === "green") {
        if (word[position] !== letter) {
          match = false;
          break;
        }
      }
      if (colour === "yellow") {
        if (!word.includes(letter) || word[position] === letter) {
          match = false;
          break;
        }
      }
    }
    return match;
  });
};

Secondly, a couple of functions to recursively create those probability trees:

const colours = ["green", "yellow", "black"];

const calculateLetterColor = (wordList, letter, position, colour) => {
  const matchingWords = matchesFilters(wordList, [
    { colour, position, letter },
  ]);
  return {
    p: (matchingWords.length * 1.0) / wordList.length,
    list: matchingWords,
  };
};

const createObject = (word, obj, depth) => {
  // Recursively create probability tree structure
  if (depth > 4) {
    return obj;
  } else {
    // For each colour, add probabilities and new lists
    colours.forEach((colour) => {
      if (!obj[colour] && obj.list.length > 0) {
        obj[colour] = calculateLetterColor(
          obj.list,
          word[depth],
          depth,
          colour
        );
      }
    });
    const newDepth = depth + 1;
    colours.forEach((colour) => {
      if (obj.list.length > 0) {
        createObject(word, obj[colour], newDepth);
      }
    });
  }
};

const fillInObject = (word, originalList) => {
  let depth = 0;
  let composedObj = { list: originalList, p: 1 };
  createObject(word, composedObj, depth);
  return composedObj;
};

And finally, a couple of functions to recursively go through those trees and do the SUMPRODUCT() of all the branches

const calculateP = (arr, obj, p, depth) => {
  colours.forEach((colour) => {
    if (obj[colour] && obj[colour].list.length > 0) {
      if (depth === 4) {
        arr.push(obj[colour].p * p);
      } else {
        calculateP(arr, obj[colour], obj[colour].p * p, depth + 1);
      }
    }
  });
};

const calculateWordScore = (obj, word) => {
  // Go through each branch in tree to multiply probabilities
  // Square each probability and add to array
  // Return the sum of the array
  const pValues = [];
  const depth = 0;
  calculateP(pValues, obj, 1, depth);
  const pSquared = pValues.map((value) => value * value);
  const score = pSquared.reduce((pv, cv) => pv + cv, 0);
  return score;
};

You can see the rest here.

Bonuses:

I did write in the code a way to do this on “Hard Mode”

If anyone finds this option more spiritually fulfilling, I can add that into the UI for you.

---

I had quite a lot of fun doing this. If you liked it, you can subscribe to see more of this kind of stuff (at least once per year!).

Alternatively, you can say hi to me on Twitter, or if you want to know more about what I do building tech for non-profits at plinth feel free to get in touch.

1. As it turns out, Wordle seems to have 2 word lists. One with ~2000 normal words, and one with 13,000 other random words I’ve never heard of (which is where the first screenshot of the solver is drawing from). Currently the solver is set to only guess vaguely sensible words (which works generally better - but you might be able to speed up the first step by guessing one of the extra 13,000: “LARES”). I suppose the optimum solver would use all 15,000 allowed words in order to guess the best possible option from among the ~2,000 normal words.